Supercell (electron–phonon)

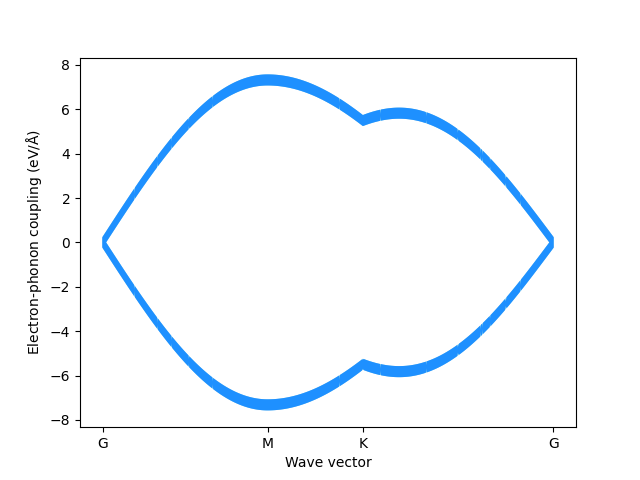
#!/usr/bin/env python3

# Copyright (C) 2017-2025 elphmod Developers
# This program is free software under the terms of the GNU GPLv3 or later.

import elphmod
import matplotlib.pyplot as plt
import numpy as np

nu = 1 # displacement direction

use_model = True # or run phrenorm_graphene first

N = [ # 3 x 3 (60 degrees instead of 120 degrees)
    [3, 0, 0],
    [3, 3, 0],
    [0, 0, 1],
]

if use_model:
    import elphmod.models.graphene

    elphmod.models.graphene.create('data/graphene')

    el = elphmod.el.Model('data/graphene')
    ph = elphmod.ph.Model('data/graphene.ifc')
    elph = elphmod.elph.Model('data/graphene.epmatwp', 'data/graphene.wigner',
        el, ph, divide_mass=False)
else:
    el = elphmod.el.Model('phrenorm_graphene/graphene')
    ph = elphmod.ph.Model('phrenorm_graphene/dfpt.ifc', apply_asr_simple=True)
    elph = elphmod.elph.Model('phrenorm_graphene/dfpt.epmatwp',
        'phrenorm_graphene/wigner.fmt', el, ph, divide_mass=False)

elph.data *= elphmod.misc.Ry / elphmod.misc.a0

ElPh = elph.supercell(*N, shared_memory=False)

path = 'GMKG'
k, x, corners = elphmod.bravais.path(path, ibrav=4, N=300)
K = np.dot(np.dot(k, elphmod.bravais.reciprocals(*elph.ph.a)), ElPh.ph.a.T)

I = elphmod.MPI.comm.Split(elphmod.MPI.comm.rank)

def g(k1=0.0, k2=0.0, k3=0.0):
    return elph.g(q1=0.0, q2=0.0, q3=0.0, k1=k1, k2=k2, k3=k3,
        comm=I)[nu]

def G(K1=0.0, K2=0.0, K3=0.0):
    return ElPh.g(q1=0.0, q2=0.0, q3=0.0, k1=K1, k2=K2, k3=K3,
        comm=I)[nu::ph.size].sum(axis=0)

g, u = elphmod.dispersion.dispersion(g, k, vectors=True)
G, U = elphmod.dispersion.dispersion(G, K, vectors=True)

w = np.ones(g.shape)
W = elphmod.dispersion.unfolding_weights(k, ElPh.cells, u, U)

linewidth = 0.5

if elphmod.MPI.comm.rank == 0:
    for n in range(g.shape[1]):
        fatband, = elphmod.plot.compline(x, g[:, n], linewidth * w[:, n])

        plt.fill(*fatband, linewidth=0.0, color='skyblue')

    for n in range(G.shape[1]):
        fatband, = elphmod.plot.compline(x, G[:, n], linewidth * W[:, n])

        plt.fill(*fatband, linewidth=0.0, color='dodgerblue')

    plt.ylabel(r'Electron-phonon coupling ($\mathrm{eV/\AA}$)')
    plt.xlabel('Wave vector')
    plt.xticks(x[corners], path)
    plt.savefig('supercell_elph.png')
    plt.show()