#!/usr/bin/env python3
# Copyright (C) 2017-2026 elphmod Developers
# This program is free software under the terms of the GNU GPLv3 or later.
import elphmod
import matplotlib.pyplot as plt
import numpy as np
nu = 8 # ionic displacement
a = 0 # electronic orbital
el = elphmod.el.Model('TaS2')
ph = elphmod.ph.Model('dfpt.dyn', apply_asr_simple=True)
elph = elphmod.elph.Model('dfpt.epmatwp', 'wigner.fmt', el, ph,
divide_mass=False)
path = 'GMKG'
k, x, corners = elphmod.bravais.path(path, ibrav=4)
g = np.empty(len(k), dtype=complex)
for ik, (k1, k2, k3) in enumerate(k):
g[ik] = elph.g(k1=k1, k2=k2, k3=k3)[nu, a, a]
g *= elphmod.misc.Ry / elphmod.misc.a0
if elphmod.MPI.comm.rank == 0:
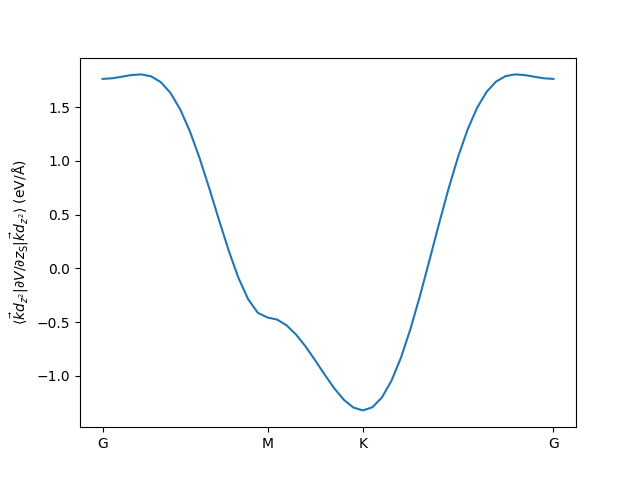
plt.ylabel(r'$\langle \vec k d_{z^2}| '
r'\partial V / \partial z_{\mathrm{S}} '
r'|\vec k d_{z^2} \rangle$ '
r'($\mathrm{eV/\AA}$)')
plt.xticks(x[corners], path)
plt.plot(x, g.real)
plt.savefig('defpot.png')
plt.show()