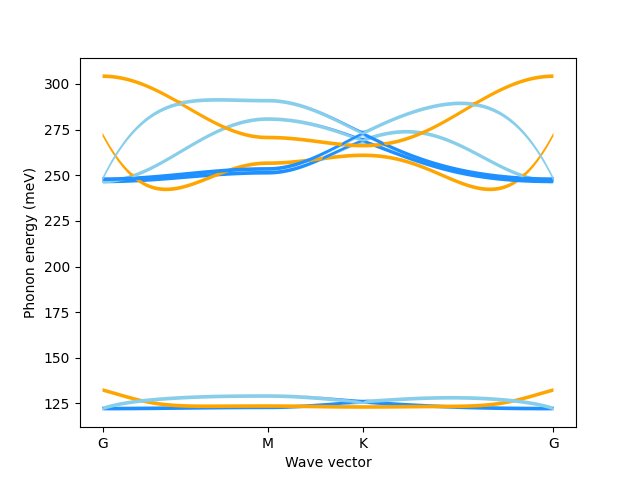
Bare phonons

This example will show you how to calculate a bare phonon dispersion, excluding any response of the electron density to displacements of the (pseudo-)ions. This is the limit of constrained density-functional perturbation theory (cDFPT) where all electronic states are in the active subspace. Note the bare Born effective charges and corresponding long-range terms and the broken acoustic sum rules.

For the bare phonons, you need a modified version of Quantum ESPRESSO. You can use the provided patches to apply the required changes.

#!/usr/bin/env python3

# Copyright (C) 2017-2025 elphmod Developers
# This program is free software under the terms of the GNU GPLv3 or later.

import elphmod
import matplotlib.pyplot as plt
import scipy.optimize

comm = elphmod.MPI.comm

colors = ['skyblue', 'dodgerblue', 'orange']

ph = elphmod.ph.Model('dyn.xml')

def cost(L):
    ph.L, = L
    ph.update_short_range()
    return ph.sum_force_constants()

scipy.optimize.minimize(cost, [10.0])

path = 'GMKG'
q, x, corners = elphmod.bravais.path(path, ibrav=4, N=300)

w2, u, order = elphmod.dispersion.dispersion(ph.D, q,
    vectors=True, order=True)

if comm.rank == 0:
    w = elphmod.ph.sgnsqrt(w2) * elphmod.misc.Ry * 1e3

    pol = elphmod.ph.polarization(u, q)

    for nu in range(ph.size):
        fatbands = elphmod.plot.compline(x, w[:, nu], 2 * pol[:, nu])

        for fatband, color in zip(fatbands, colors):
            plt.fill(*fatband, color=color, linewidth=0.0)

    plt.ylabel('Phonon energy (meV)')
    plt.xlabel('Wave vector')
    plt.xticks(x[corners], path)
    plt.savefig('bare.png')
    plt.show()