Dimerization (carbon chain)

This example shows how to

• create a low-energy model for a one-dimensional system (downfolding),

• simulate the periodic (Peierls) lattice distortion in this model.

#!/usr/bin/env python3

# Copyright (C) 2017-2025 elphmod Developers
# This program is free software under the terms of the GNU GPLv3 or later.

import elphmod
import matplotlib.pyplot as plt
import scipy.optimize

el = elphmod.el.Model('C', rydberg=True)
ph = elphmod.ph.Model('dyn.xml', divide_mass=False, apply_asr_simple=True)
elph = elphmod.elph.Model('work/C.epmatwp', 'wigner.fmt',
    el, ph, divide_mass=False)

elph = elph.supercell(1, 1, 2)

driver = elphmod.md.Driver(elph, kT=0.02, f=elphmod.occupations.gauss,
    nk=(1, 1, 100), nq=(1, 1, 4), n=elph.el.size)

driver.kT = 0.002

driver.random_displacements(reproducible=True)

driver.plot(interactive=True, scale=25, elev=0)

scipy.optimize.minimize(driver.free_energy, driver.u, jac=driver.jacobian,
    method='BFGS', tol=1e-8)

driver.plot(interactive=False)
driver.plot(filename='cdw_1d_1.png')

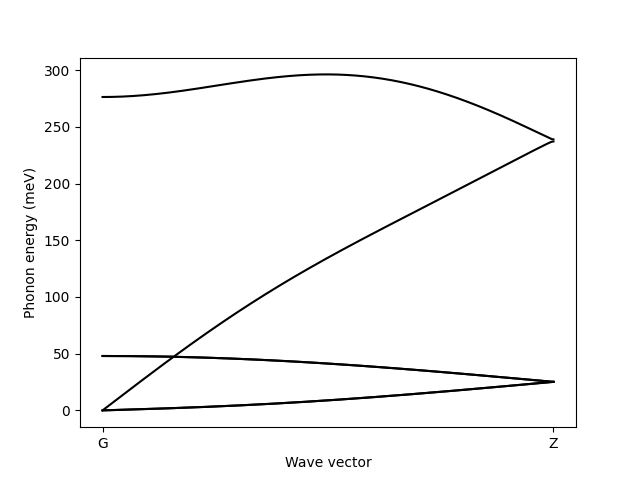
ph = driver.phonons()

path = 'GZ'
q, x, corners = elphmod.bravais.path(path, ibrav=6, N=1000)

w2 = elphmod.dispersion.dispersion(ph.D, q)

if elphmod.MPI.comm.rank == 0:
    w = elphmod.ph.sgnsqrt(w2) * elphmod.misc.Ry * 1e3

    plt.plot(x, w, 'k')
    plt.ylabel('Phonon energy (meV)')
    plt.xlabel('Wave vector')
    plt.xticks(x[corners], path)
    plt.savefig('cdw_1d_2.png')
    plt.show()