#!/usr/bin/env python3
# Copyright (C) 2017-2026 elphmod Developers
# This program is free software under the terms of the GNU GPLv3 or later.
import elphmod.models.chain
import matplotlib.pyplot as plt
import numpy as np
comm = elphmod.MPI.comm
info = elphmod.MPI.info
nq = 240
eta = 0.05 / elphmod.misc.Ry
info('Set up model and sample data')
el, ph, elph = elphmod.models.chain.create('data/chain', rydberg=True)
k = q = np.linspace(0, 2 * np.pi, nq, endpoint=False)
e, U = elphmod.dispersion.dispersion(el.H, q, vectors=True)
w2, u = elphmod.dispersion.dispersion(ph.D, q, vectors=True)
g2 = np.empty((len(q), ph.size, len(k), el.size, el.size))
for iq in range(len(q)):
for ik in range(len(k)):
g2[iq, :, ik, :, :] = abs(np.einsum('xu,am,xab,bn->xmn', u[iq],
U[(ik + iq) % nq].conj(), elph.g(q1=q[iq], k1=k[ik]), U[ik])) ** 2
w = elphmod.ph.sgnsqrt(w2)
w[0, :3] = eta # avoid division by zero acoustic frequency
g2 /= 2 * w[:, :, np.newaxis, np.newaxis, np.newaxis]
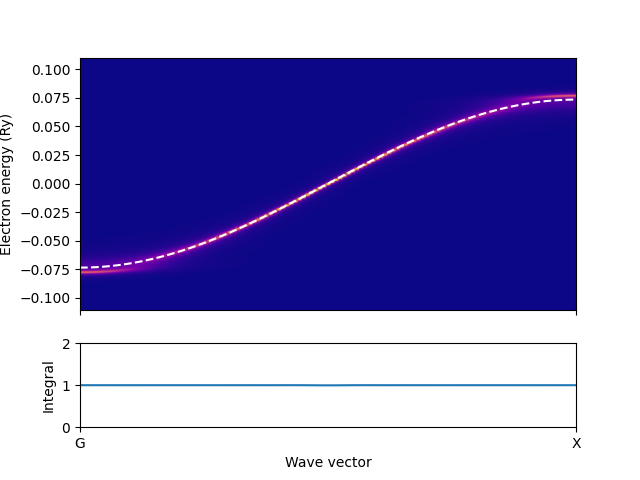
info('Calculate spectral function')
kT = 1000 * elphmod.misc.kB / elphmod.misc.Ry
omega, domega = np.linspace(1.5 * e.min(), 1.5 * e.max(), nq, retstep=True)
Sigma = elphmod.diagrams.fan_migdal_self_energy(k.reshape((-1, 1)), e, w, g2,
omega + 1j * eta, kT)
G = 1 / (omega[np.newaxis, np.newaxis, :] - e[:, :, np.newaxis] - Sigma)
A = -G.imag / np.pi
integral = A.sum(axis=2) * domega
if comm.rank == 0:
ik = nq // 2 + 1
fig, (ax1, ax2) = plt.subplots(2, 1, sharex=True,
gridspec_kw=dict(height_ratios=(3, 1)))
ax1.set_ylabel('Electron energy (Ry)')
ax2.set_ylabel('Integral')
ax2.set_xlabel('Wave vector')
ax2.set_xticks([0.0, np.pi])
ax2.set_xticklabels('GX')
ax1.imshow(A[:ik, 0, ::-1].T, extent=(0.0, np.pi, omega[0], omega[-1]),
cmap='plasma')
ax1.plot(k[:ik], e[:ik], 'w--')
ax1.axis('auto')
ax2.plot(k[:ik], integral[:ik, 0])
ax2.set_ylim(0.0, 2 * el.size)
plt.savefig('fan_migdal_1.png')
plt.show()
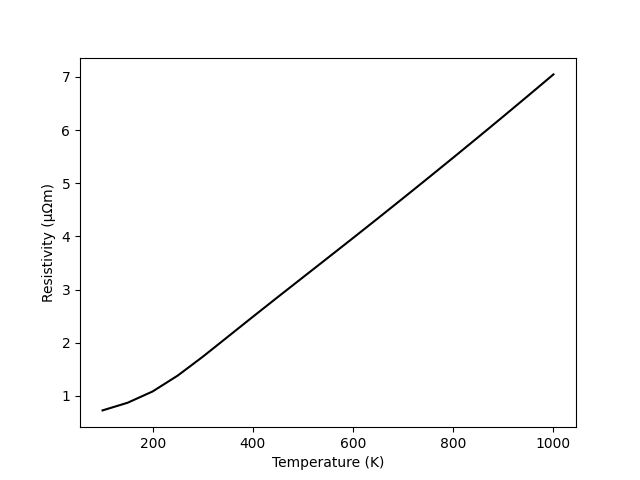
info('Calculate resistivity')
v = elphmod.dispersion.sample(el.v, q)
v = np.einsum('ix,kan,kiab,kbn->knx', ph.a, U.conj(), v, U)[:, :, :1].real
kT = np.arange(100, 1050, 50) * elphmod.misc.kB / elphmod.misc.Ry
sigma = np.empty(len(kT))
for ikT in range(len(kT)):
fsthick = 6.9 * kT[ikT]
domega = 0.1 * eta
omega = np.arange(np.ceil(-fsthick / domega) * domega, fsthick, domega)
Sigma = elphmod.diagrams.fan_migdal_self_energy(q.reshape((-1, 1)),
e, w, g2, omega + 1j * eta, kT[ikT])
G = 1 / (omega[np.newaxis, np.newaxis, :] - e[:, :, np.newaxis] - Sigma)
A = -G.imag / np.pi
sigma[ikT] = elphmod.diagrams.green_kubo_conductivity(v, A, omega,
kT[ikT], a=ph.a, dc_only=True)[0, 0]
if comm.rank == 0:
plt.plot(kT / elphmod.misc.kB * elphmod.misc.Ry,
1e6 / elphmod.misc.ohmmRy / sigma, 'k')
plt.ylabel('Resistivity (\u03bc\u03a9m)')
plt.xlabel('Temperature (K)')
plt.savefig('fan_migdal_2.png')
plt.show()