Occupations

#!/usr/bin/env python3

# Copyright (C) 2017-2025 elphmod Developers
# This program is free software under the terms of the GNU GPLv3 or later.

from elphmod import MPI, occupations
import matplotlib.pyplot as plt
import numpy as np

if MPI.comm.rank:
    raise SystemExit

x = np.linspace(-10, 10, 2001)

style = dict(color='lightgray', linestyle='dashed')

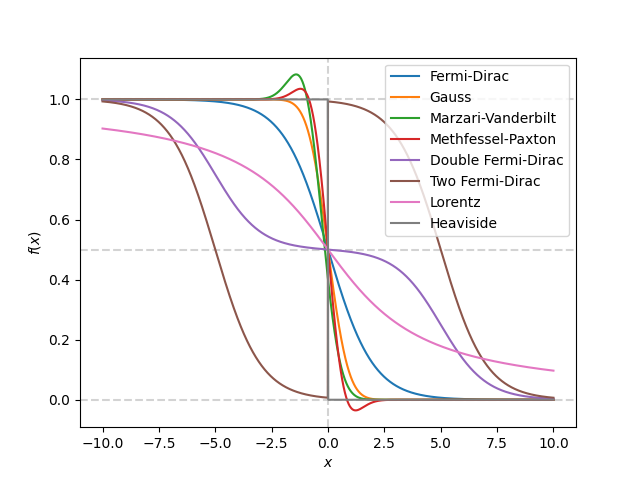
print('Plot step functions')

plt.axvline(x=0.0, **style)
plt.axhline(y=0.0, **style)
plt.axhline(y=0.5, **style)
plt.axhline(y=1.0, **style)

plt.plot(x, occupations.fermi_dirac(x), label='Fermi-Dirac')
plt.plot(x, occupations.gauss(x), label='Gauss')
plt.plot(x, occupations.marzari_vanderbilt(x), label='Marzari-Vanderbilt')
plt.plot(x, occupations.methfessel_paxton(x), label='Methfessel-Paxton')
plt.plot(x, occupations.double_fermi_dirac(x), label='Double Fermi-Dirac')
plt.plot(x, occupations.two_fermi_dirac(x), label='Two Fermi-Dirac')
plt.plot(x, occupations.lorentz(x), label='Lorentz')
plt.plot(x, occupations.heaviside(x), label='Heaviside')

plt.xlabel(r'$x$')
plt.ylabel(r'$f(x)$')
plt.legend()
plt.savefig('occupations_1.png')
plt.show()

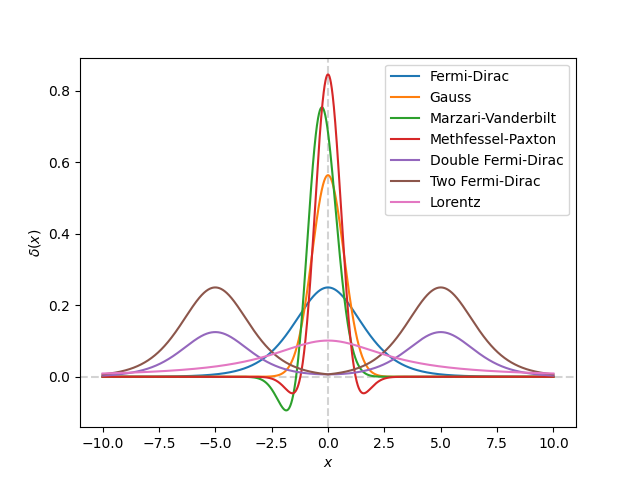
print('Plot delta functions')

plt.axvline(x=0.0, **style)
plt.axhline(y=0.0, **style)

plt.plot(x, occupations.fermi_dirac.delta(x), label='Fermi-Dirac')
plt.plot(x, occupations.gauss.delta(x), label='Gauss')
plt.plot(x, occupations.marzari_vanderbilt.delta(x), label='Marzari-Vanderbilt')
plt.plot(x, occupations.methfessel_paxton.delta(x), label='Methfessel-Paxton')
plt.plot(x, occupations.double_fermi_dirac.delta(x), label='Double Fermi-Dirac')
plt.plot(x, occupations.two_fermi_dirac.delta(x), label='Two Fermi-Dirac')
plt.plot(x, occupations.lorentz.delta(x), label='Lorentz')

plt.xlabel(r'$x$')
plt.ylabel(r'$\delta(x)$')
plt.legend()
plt.savefig('occupations_2.png')
plt.show()

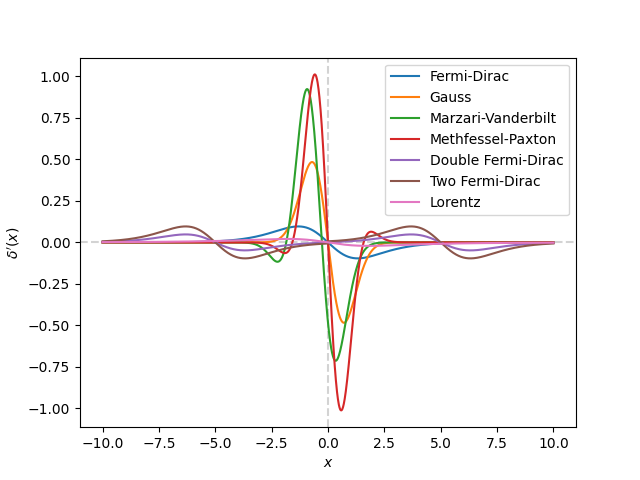
print('Plot derivatives of delta functions')

plt.axvline(x=0.0, **style)
plt.axhline(y=0.0, **style)

plt.plot(x, occupations.fermi_dirac.delta_prime(x), label='Fermi-Dirac')
plt.plot(x, occupations.gauss.delta_prime(x), label='Gauss')
plt.plot(x, occupations.marzari_vanderbilt.delta_prime(x),
    label='Marzari-Vanderbilt')
plt.plot(x, occupations.methfessel_paxton.delta_prime(x),
    label='Methfessel-Paxton')
plt.plot(x, occupations.double_fermi_dirac.delta_prime(x),
    label='Double Fermi-Dirac')
plt.plot(x, occupations.two_fermi_dirac.delta_prime(x), label='Two Fermi-Dirac')
plt.plot(x, occupations.lorentz.delta_prime(x), label='Lorentz')

plt.xlabel(r'$x$')
plt.ylabel(r"$\delta'(x)$")
plt.legend()
plt.savefig('occupations_3.png')
plt.show()

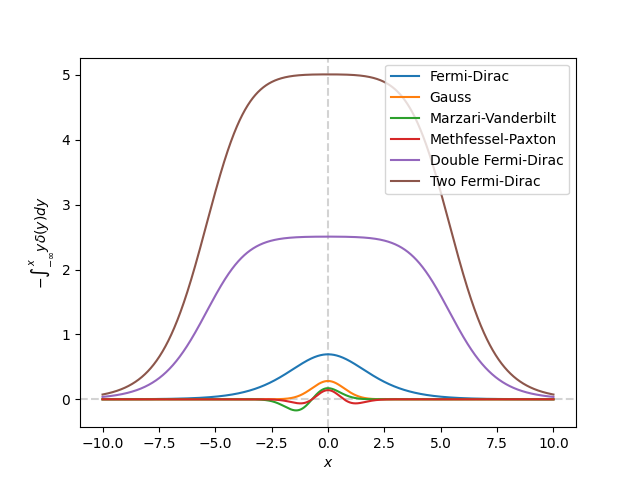
print('Plot generalized entropy')

plt.axvline(x=0.0, **style)
plt.axhline(y=0.0, **style)

plt.plot(x, occupations.fermi_dirac.entropy(x), label='Fermi-Dirac')
plt.plot(x, occupations.gauss.entropy(x), label='Gauss')
plt.plot(x, occupations.marzari_vanderbilt.entropy(x),
    label='Marzari-Vanderbilt')
plt.plot(x, occupations.methfessel_paxton.entropy(x), label='Methfessel-Paxton')
plt.plot(x, occupations.double_fermi_dirac.entropy(x),
    label='Double Fermi-Dirac')
plt.plot(x, occupations.two_fermi_dirac.entropy(x), label='Two Fermi-Dirac')

plt.xlabel(r'$x$')
plt.ylabel(r'$-\int_{-\infty}^x y \delta(y) dy$')
plt.legend()
plt.savefig('occupations_4.png')
plt.show()