#!/usr/bin/env python3
# Copyright (C) 2017-2026 elphmod Developers
# This program is free software under the terms of the GNU GPLv3 or later.
# See Allen and Dynes, Phys. Rev. B 12, 905 (1975) for the formulas used here.
import elphmod.models.graphene
import matplotlib.pyplot as plt
import numpy as np
comm = elphmod.MPI.comm
nk = nq = 36
kTel = 0.3
kTph = 0.0015
f = elphmod.occupations.fermi_dirac
eps = 1e-10
el, ph, elph, elel = elphmod.models.graphene.create()
ph.data *= elphmod.misc.Ry ** 2
elph.data *= elphmod.misc.Ry ** 1.5
q = sorted(elphmod.bravais.irreducibles(nq))
weights = np.array([len(elphmod.bravais.images(q1, q2, nq)) for q1, q2 in q])
q = 2 * np.pi / nq * np.array(q)
e, U = elphmod.dispersion.dispersion_full_nosym(el.H, nk, vectors=True)
e = e[..., :1]
U = U[..., :1]
w2, u = elphmod.dispersion.dispersion(ph.D, q, vectors=True)
dangerous = np.where(w2 < eps)
w2[dangerous] = eps
w = elphmod.ph.sgnsqrt(w2)
g2 = elph.sample(q, U=U, u=u, squared=True, shared_memory=True)
g2dd, dd = elphmod.diagrams.double_fermi_surface_average(q, e, g2, kTel, f)
g2dd[dangerous] = 0.0
g2dd /= 2 * w
omega, domega = np.linspace(0.0, 1.1 * w.max(), 500,
endpoint=False, retstep=True)
omega += domega / 2
sizes, bounds = elphmod.MPI.distribute(len(omega), bounds=True, comm=comm)
my_DOS = np.empty(sizes[comm.rank])
my_a2F = np.empty(sizes[comm.rank])
for my_n, n in enumerate(range(*bounds[comm.rank:comm.rank + 2])):
x = (w - omega[n]) / kTph
my_DOS[my_n] = (weights[:, np.newaxis] * f.delta(x) / kTph).sum()
my_a2F[my_n] = (weights[:, np.newaxis] * f.delta(x) / kTph * g2dd).sum()
my_DOS /= weights.sum()
my_a2F /= (weights * dd).sum()
N0 = f.delta(e / kTel).sum() / kTel / np.prod(e.shape[:-1])
my_a2F *= N0
DOS = np.empty(len(omega))
a2F = np.empty(len(omega))
comm.Allgatherv(my_DOS, (DOS, sizes))
comm.Allgatherv(my_a2F, (a2F, sizes))
lamda, wlog, Tc = elphmod.eliashberg.McMillan(nq, e, w2, g2, mustar=0.0,
kT=kTel, f=f)
if elphmod.MPI.comm.rank == 0:
nph_int = DOS.sum() * domega
lamda_int = 2 * (a2F / omega).sum() * domega
wlog_int = np.exp(2 / lamda_int
* (a2F / omega * np.log(omega)).sum() * domega)
print('integrals (sums):')
print('states = %g (%g)' % (nph_int, ph.size))
print('lambda = %g (%g)' % (lamda_int, lamda))
print('omega_log = %g eV (%g eV)' % (wlog_int, wlog))
fig, ax1 = plt.subplots()
ax2 = ax1.twinx()
ax1.set_xlabel('Phonon energy (eV)')
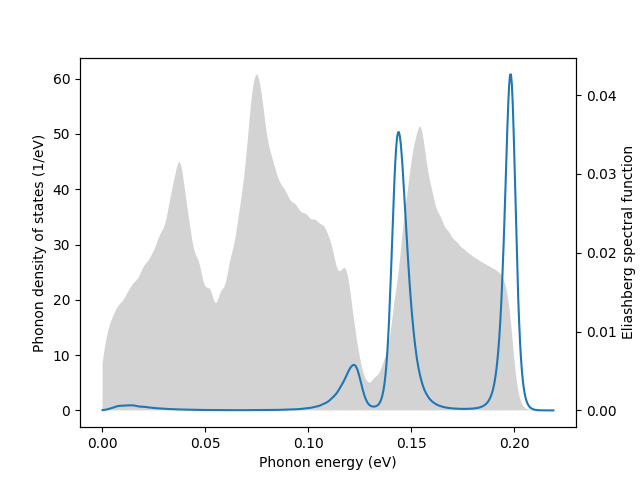
ax1.set_ylabel('Phonon density of states (1/eV)')
ax2.set_ylabel('Eliashberg spectral function')
ax1.fill_between(omega, 0.0, DOS, facecolor='lightgray')
ax2.plot(omega, a2F)
plt.savefig('a2f.png')
plt.show()