Kekulé distortion

#!/usr/bin/env python3

# Copyright (C) 2017-2025 elphmod Developers
# This program is free software under the terms of the GNU GPLv3 or later.

import elphmod.models.graphene
import matplotlib.pyplot as plt
import numpy as np
import scipy.optimize

comm = elphmod.MPI.comm

sparse = False # use sparse matrices to be able to simulate large cells?

N = 6
nk = 6
nq = 6

kT0 = 2.0
kT = 0.02

elphmod.models.graphene.create('data/graphene')

el = elphmod.el.Model('data/graphene', rydberg=True)
ph = elphmod.ph.Model('data/graphene.ifc', divide_mass=False)
elph = elphmod.elph.Model('data/graphene.epmatwp', 'data/graphene.wigner',
    el, ph, divide_mass=False)

elph.data *= 1.5 # otherwise the system is stable

if not sparse:
    elph = elph.supercell(N, N)

    nk //= N
    nq //= N

driver = elphmod.md.Driver(elph, kT=kT0, f=elphmod.occupations.fermi_dirac,
    nk=(nk, nk), nq=(nq, nq), supercell=(N, N) if sparse else None,
    n=elph.el.size)

driver.kT = kT

driver.random_displacements(amplitude=0.05, reproducible=True)

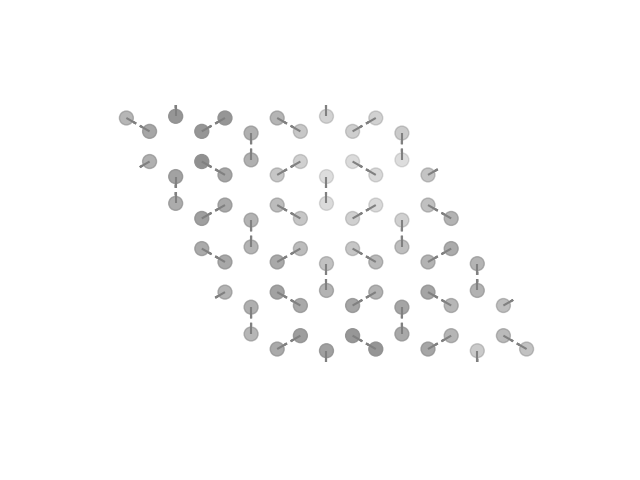
driver.plot(interactive=True)

scipy.optimize.minimize(driver.free_energy, driver.u, jac=driver.jacobian,
    method='BFGS', options=dict(gtol=1e-8, norm=np.inf))

driver.plot(interactive=False)
driver.plot(filename='kekule_1.png')

path = 'GMKG'
k, x, corners = elphmod.bravais.path(path, ibrav=4, N=150)
q = k

el = driver.electrons()

e = elphmod.dispersion.dispersion(el.H, k)

if comm.rank == 0:
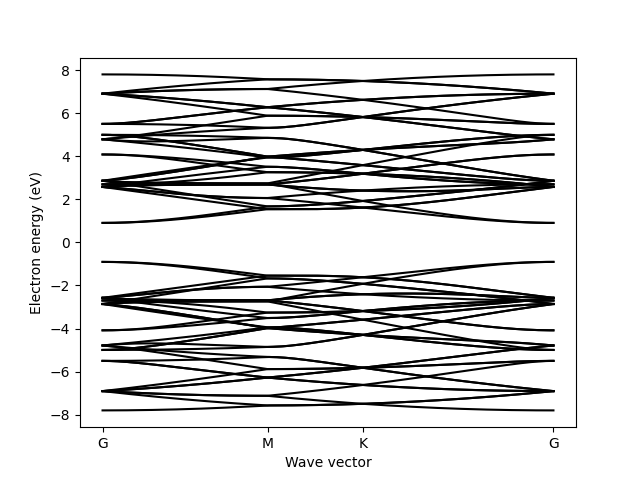
    plt.plot(x, e, 'k')
    plt.ylabel('Electron energy (eV)')
    plt.xlabel('Wave vector')
    plt.xticks(x[corners], path)
    plt.savefig('kekule_2.png')
    plt.show()

ph = driver.phonons()

w2 = elphmod.dispersion.dispersion(ph.D, q)

if comm.rank == 0:
    w = elphmod.ph.sgnsqrt(w2) * elphmod.misc.Ry * 1e3

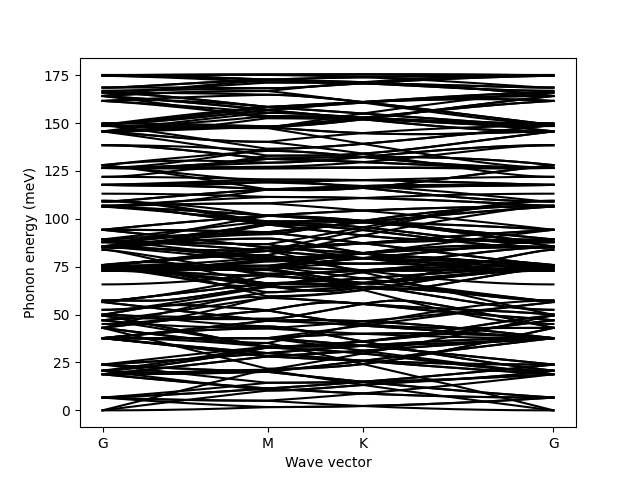
    plt.plot(x, w, 'k')
    plt.ylabel('Phonon energy (meV)')
    plt.xlabel('Wave vector')
    plt.xticks(x[corners], path)
    plt.savefig('kekule_3.png')
    plt.show()

u1 = driver.u.copy()

if not np.any(abs(u1) > 1e-2):
    raise SystemExit

alpha = np.linspace(-1.5, 1.5, 301)
E = np.empty_like(alpha)

i0 = np.argmin(abs(alpha))
i1 = np.argmin(abs(alpha - 1))

for i in range(len(alpha)):
    driver.u = alpha[i] * u1
    E[i] = driver.free_energy()

    if i == i0:
        c0 = 0.5 * u1.T.dot(driver.hessian()).dot(u1)
    elif i == i1:
        c1 = 0.5 * u1.T.dot(driver.hessian()).dot(u1)

if comm.rank == 0:
    scale = 1e3 * elphmod.misc.Ry / len(driver.elph.cells)

    E -= E[i0]
    E *= scale

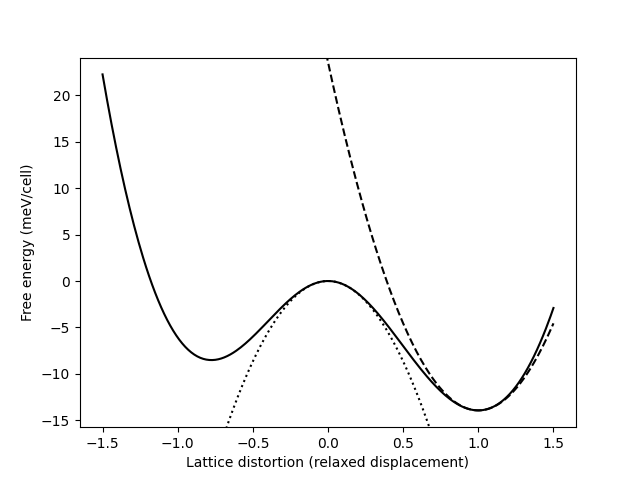
    plt.plot(alpha, E, 'k')

    c0 *= scale
    c1 *= scale

    ylim = plt.ylim()
    plt.plot(alpha, c0 * (alpha - alpha[i0]) ** 2 + E[i0], 'k:')
    plt.plot(alpha, c1 * (alpha - alpha[i1]) ** 2 + E[i1], 'k--')
    plt.ylim(ylim)

    plt.ylabel('Free energy (meV/cell)')
    plt.xlabel('Lattice distortion (relaxed displacement)')
    plt.savefig('kekule_4.png')
    plt.show()