Goldstone modes
The movement of the atoms of a diatomic molecule can be classified into the following six eigenmodes:
one bond-stretching mode,
three translational modes,
two rotational modes.
Only the first mode has a nonzero vibration frequency. Since the presence of the molecule breaks the homogeneity and isotropy (except for a rotation about the bond axis) of the space (or: since the total energy must be invariant with respect to a rigid translation or rotation of the molecule), the remaining five modes are Goldstone bosons with zero energy (or: without any restoring force).
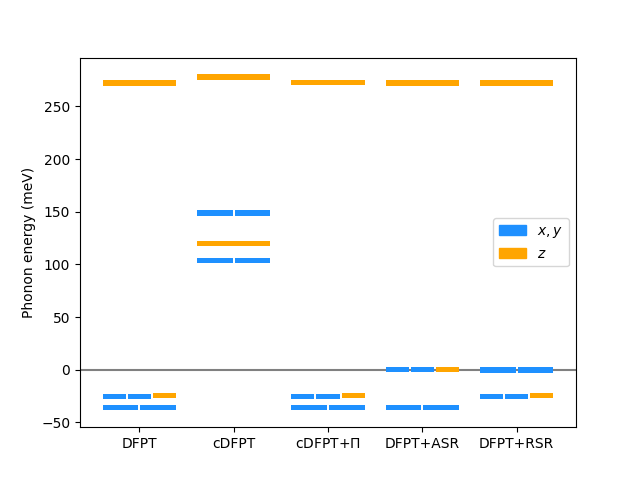
Using the example of a nitrogen molecule, this example shows that
cDFPT phonons do not always satisfy the Goldstone theorem [van Loon et al., Phys. Rev. B 103, 205103 (2021)],
the acoustic sum rule correction restores the translational Goldstone modes,
the Born-Huang sum rule correction restores the rotational Goldstone modes.
The example also shows how to calculate exact DFPT phonon self-energies for gapped systems (i.e., without any electronic occupation smearing).
For the (c)DFPT part, you need a modified version of Quantum ESPRESSO. You can use the provided patches to apply the required changes.
The results obtained in this example are far from converged!
#!/usr/bin/env python3
# Copyright (C) 2017-2026 elphmod Developers
# This program is free software under the terms of the GNU GPLv3 or later.
import elphmod
import matplotlib.patches as pts
import matplotlib.pyplot as plt
import numpy as np
colors = ['dodgerblue', 'orange']
labels = ['$x, y$', '$z$']
e = elphmod.el.read_pwo('pw.out')[0][0]
nel = len(e)
e = e.reshape((1, 1, nel))
ph = dict()
d = dict()
for method in 'cdfpt', 'dfpt':
ph[method] = elphmod.ph.Model(method + '.ifc')
ph[method].data *= elphmod.misc.Ry ** 2
nph = ph[method].size
d[method] = elphmod.elph.read_xml_files(method + '.phsave/elph.%d.%d.xml',
q=1, rep=nph, bands=range(nel), nbands=nel, nk=1, status=False)
d[method] *= elphmod.misc.Ry ** 1.5
ph['dfpt_asr'] = elphmod.ph.Model('dfpt.ifc', apply_asr=True)
ph['dfpt_asr'].data *= elphmod.misc.Ry ** 2
ph['dfpt_rsr'] = elphmod.ph.Model('dfpt.ifc', apply_rsr=True)
ph['dfpt_rsr'].data *= elphmod.misc.Ry ** 2
q = np.array([[0, 0]])
Pi = elphmod.diagrams.phonon_self_energy(q, e, g=d['cdfpt'], G=d['dfpt'],
occupations=elphmod.occupations.heaviside).reshape((nph, nph))
if elphmod.MPI.comm.rank != 0:
raise SystemExit
D = [
ph['dfpt'].D(),
ph['cdfpt'].D(),
ph['cdfpt'].D() + Pi / ph['dfpt'].M[0],
ph['dfpt_asr'].D(),
ph['dfpt_rsr'].D(),
]
Shorten = 0.1
shorten = 0.01
width = 5.0
plt.axhline(0.0, color='gray', zorder=0)
for n in range(len(D)):
X1 = n - 0.5 + Shorten
X2 = n + 0.5 - Shorten
w2, u = np.linalg.eigh(D[n])
w = elphmod.ph.sgnsqrt(w2) * 1e3
Z = (abs(u[2::3]) ** 2).sum(axis=0) > 0.5
for group in elphmod.misc.group(w, eps=1.1 * width):
N = len(group)
for i, nu in enumerate(group):
x1 = (i * X2 + (N - i) * X1) / N + shorten; i += 1
x2 = (i * X2 + (N - i) * X1) / N - shorten
plt.fill_between([x1, x2], w[nu] - 0.5 * width, w[nu] + 0.5 * width,
linewidth=0.0, color=colors[int(Z[nu])])
plt.ylabel('Phonon energy (meV)')
plt.xticks(range(len(D)),
['DFPT', 'cDFPT', r'cDFPT+$\Pi$', 'DFPT+ASR', 'DFPT+RSR'])
plt.legend(handles=[pts.Patch(color=color, label=label)
for color, label in zip(colors, labels)])
plt.savefig('goldstone.png')
plt.show()