Phonon renormalization (α-Po)

This example shows how to

• perform a cDFPT calculation [Nomura & Arita, PRB 92, 245108 (2015)],

• work with electrons, phonons, and their coupling in localized bases,

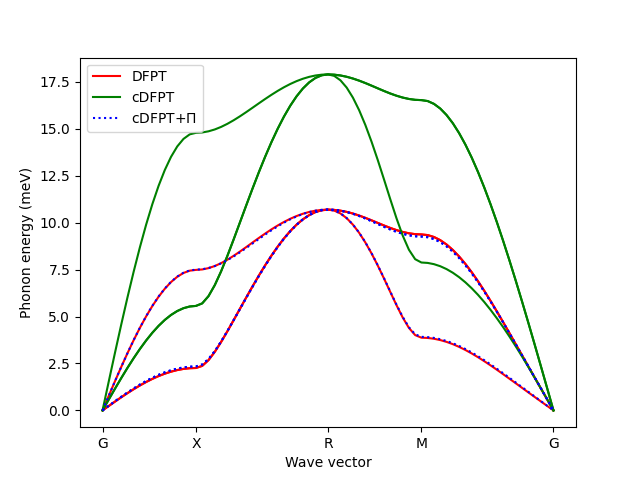
• consistently renormalize phonon dispersions (go from cDFPT to DFPT).

For the cDFPT part, you need a modified version of Quantum ESPRESSO. You can use the provided patches to apply the required changes.

The results obtained in this example are very far from converged! In return, the ab initio part takes less than a minute on a laptop with only two cores.

#!/usr/bin/env python3

# Copyright (C) 2017-2025 elphmod Developers
# This program is free software under the terms of the GNU GPLv3 or later.

import copy
import elphmod
import matplotlib.pyplot as plt
import numpy as np

comm = elphmod.MPI.comm
info = elphmod.MPI.info

PW = elphmod.bravais.read_pwi('scf.in')
PH = elphmod.bravais.read_ph('dfpt.in')

kT = PW['degauss'] * elphmod.misc.Ry
f = elphmod.occupations.smearing(**PW)

nk = PW['k_points'][:3]
nq = [PH['nq1'], PH['nq2'], PH['nq3']]

info('Prepare wave vectors')

k = elphmod.bravais.mesh(*nk)
q = elphmod.bravais.mesh(*nq)

q_flat = np.reshape(q, (-1, 3))

path = 'GXRMG'
q_path, x, corners = elphmod.bravais.path(path, N=100, moveG=1e-3, **PW)

info('Prepare electrons')

el = elphmod.el.Model('polonium')
mu = elphmod.el.read_Fermi_level('scf.out')

e, U = elphmod.dispersion.dispersion(el.H, k, vectors=True)
e -= mu

info('Prepare phonons')

ph = dict()

for method in 'cdfpt', 'dfpt':
    ph[method] = elphmod.ph.Model('%s.dyn' % method, apply_asr_simple=True,
        lr=False)

info('Prepare electron-phonon coupling')

g = dict()

for method in sorted(ph):
    elph = elphmod.elph.Model('%s.epmatwp' % method, 'wigner.fmt',
        el, ph['cdfpt'])

    g[method] = elph.sample(q_flat, U=U) * elphmod.misc.Ry ** 1.5

info('Calculate phonon self-energy')

Pi = elphmod.diagrams.phonon_self_energy(q_flat, e, g=g['cdfpt'], G=g['dfpt'],
    kT=kT, occupations=f)
Pi = np.reshape(Pi, (nq[0], nq[1], nq[2], ph['cdfpt'].size, ph['cdfpt'].size))
Pi /= elphmod.misc.Ry ** 2

info('Renormalize phonons')

D = elphmod.dispersion.sample(ph['cdfpt'].D, q)

ph['cdfpt+pi'] = copy.copy(ph['dfpt'])

elphmod.ph.q2r(ph['cdfpt+pi'], D_full=D + Pi, apply_asr_simple=True)

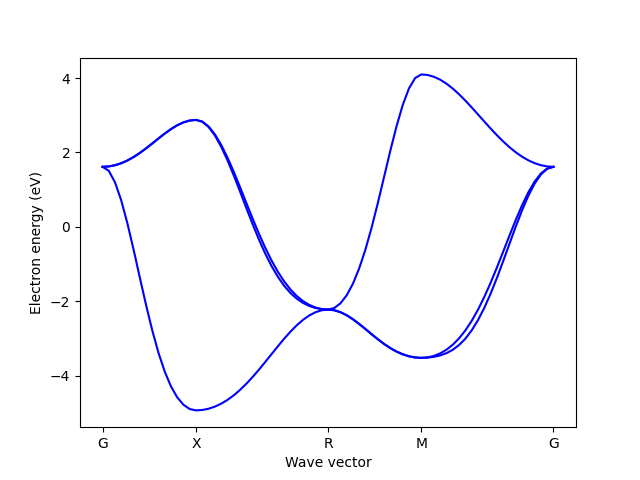
info('Plot electrons')

e = elphmod.dispersion.dispersion(el.H, q_path)
e -= mu

if comm.rank == 0:
    for n in range(el.size):
        plt.plot(x, e[:, n], 'b')

    plt.ylabel('Electron energy (eV)')
    plt.xlabel('Wave vector')
    plt.xticks(x[corners], path)
    plt.savefig('phrenorm_3d_1.png')
    plt.show()

info('Plot cDFPT, DFPT and renormalized phonons')

for method, label, style in [('dfpt', 'DFPT', 'r'), ('cdfpt', 'cDFPT', 'g'),
        ('cdfpt+pi', r'cDFPT+$\Pi$', 'b:')]:

    w2 = elphmod.dispersion.dispersion(ph[method].D, q_path)

    w = elphmod.ph.sgnsqrt(w2) * elphmod.misc.Ry * 1e3

    if comm.rank == 0:
        for nu in range(ph[method].size):
            plt.plot(x, w[:, nu], style, label=None if nu else label)

if comm.rank == 0:
    plt.ylabel('Phonon energy (meV)')
    plt.xlabel('Wave vector')
    plt.xticks(x[corners], path)
    plt.legend()
    plt.savefig('phrenorm_3d_2.png')
    plt.show()