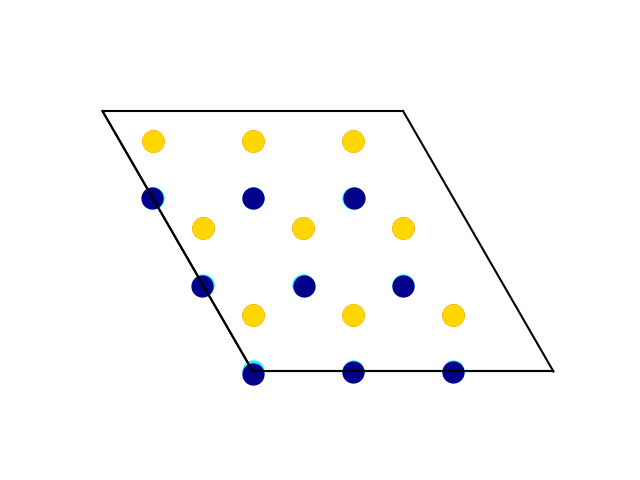
Mode decomposition
This example is still work in progress, but at the moment we can insert
the CDW supercell dimensions,
a CDW structure as a Quantum ESPRESSO input file,
associated harmonic interatomic force constants from DFPT as an .ifc file
and the code aligns the charge-density wave (CDW) and the symmetric structure.
Returns the file: info.dat
Open issues:
Decomposition of CDW modes into harmonic eigenmodes from DFPT.
It does not work for rotated structures.
#!/usr/bin/env python3
# Copyright (C) 2017-2026 elphmod Developers
# This program is free software under the terms of the GNU GPLv3 or later.
"""
Created on Sun Mar 14 15:15:43 2021
@author: arne
"""
import elphmod
import re
import numpy as np
import sys
from modes_modules import (supercell_vectors, permutation_finder,
align_structures)
import matplotlib.pyplot as plt
comm = elphmod.MPI.comm
symmetrize = True
if comm.rank == 0:
file = open('info.dat', 'w')
material = 'NbSe2'
N1 = 3
N2 = 3
cdw_path = '%s_3x3_CDW.in' % (material)
transition_metal = 'Nb'
chalcogen = 'Se'
if comm.rank == 0:
file.write('Charge-density-wave structure: %d x %d\n' % (N1, N2))
# Load symmetric structure
cdw_data = elphmod.bravais.read_pwi(cdw_path)
R_cdw = cdw_data['r']
nat = cdw_data['nat']
at_cdw = cdw_data['at']
# Load lattice parameters
A = cdw_data['a']
C = cdw_data['c']
a = A / N1
#alat = a / elphmod.misc.a0
if comm.rank == 0:
file.write('Lattice parameter of the unit cell a = %3.12f\n' % a)
# Load lattice translations
a1, a2 = elphmod.bravais.translations(two_dimensional=False)
a1 *= a
a2 *= a
a3 = np.array([0.0, 0.0, C])
# Load real space supercell vectors
A1, A2, A3 = supercell_vectors(cdw_data, N1, N2, A, a, a1, a2, a3)
# Load reciprocal space supercell vectors
B1, B2, B3 = elphmod.bravais.reciprocals(A1, A2, A3)
# Check coordinate type of input
coords_input = cdw_data['coords']
coords_type_QE = ['crystal', 'bohr', 'angstrom', 'alat']
flag_coords_type = False
for coords_type in coords_type_QE:
if re.search(coords_type, coords_input, re.IGNORECASE):
if comm.rank == 0:
file.write('Coordinates are given in %s\n' % coords_type)
flag_coords_type = True
if coords_type == 'crystal':
# Transform from crystal to cartesian coordinates
R_cdw = elphmod.bravais.crystal_to_cartesian(R_cdw, A1, A2, A3)
if not flag_coords_type:
if comm.rank == 0:
file.write('Did not find coordinate type in input file. '
'Stopping program...\n')
sys.exit()
"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""
# Load mass-spring model and setup symmetric crystal structure:
"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""
ph = elphmod.ph.Model('../data/NbSe2_DFPT.ifc', apply_asr_simple=True)
# cartesian coordinates (angstrom)
tau = ph.r * elphmod.misc.a0
# Set up sym. atomic positions from the IFC file:
R_sym = np.empty((int(round(N1)), int(round(N2)), ph.nat, 3))
for n1 in range(int(round(N1))):
for n2 in range(int(round(N2))):
R_sym[n1, n2] = a1 * n1 + a2 * n2 + tau
at_sym = []
for index in range(int(round(N1)) * int(round(N2))):
for ityp in range(3):
at_sym.append(ph.atom_order[ityp])
"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""
# Shift and align structures:
"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""
R_sym = R_sym.reshape(R_cdw.shape)
if symmetrize:
# Fold structures into supercell
R_cdw = elphmod.bravais.cartesian_to_crystal(R_cdw, A1, A2, A3)
R_sym = elphmod.bravais.cartesian_to_crystal(R_sym, A1, A2, A3)
R_cdw[:, 0] %= 1
R_cdw[:, 1] %= 1
R_sym[:, 0] %= 1
R_sym[:, 1] %= 1
R_cdw = elphmod.bravais.crystal_to_cartesian(R_cdw, A1, A2, A3)
R_sym = elphmod.bravais.crystal_to_cartesian(R_sym, A1, A2, A3)
# Align structures
R_cdw = align_structures(nat, R_cdw, R_sym, A1, A2, eps=0.5 * a)
original_atom_index = 1
distance_to_original_uc = np.empty((nat))
for atom_index in range(nat):
if at_cdw[atom_index] != at_sym[original_atom_index]:
distance_to_original_uc[atom_index] = 1e10
else:
distance_to_original_uc[atom_index] = np.linalg.norm(
R_cdw[atom_index] - R_sym[original_atom_index])
shift_index = np.argmin(distance_to_original_uc)
shift_vector = (R_cdw[np.argmin(distance_to_original_uc)]
- R_sym[original_atom_index])
R_cdw -= shift_vector
# Fold structures into supercell
R_cdw = elphmod.bravais.cartesian_to_crystal(R_cdw, A1, A2, A3)
R_sym = elphmod.bravais.cartesian_to_crystal(R_sym, A1, A2, A3)
R_cdw[:, 0] %= 1
R_cdw[:, 1] %= 1
R_sym[:, 0] %= 1
R_sym[:, 1] %= 1
R_cdw = elphmod.bravais.crystal_to_cartesian(R_cdw, A1, A2, A3)
R_sym = elphmod.bravais.crystal_to_cartesian(R_sym, A1, A2, A3)
# Align structures
R_cdw = align_structures(nat, R_cdw, R_sym, A1, A2, eps=0.5 * a)
# Calculate the barycenter
BC_sym = 0.0
BC_cdw = 0.0
for ii in range(nat):
BC_sym += R_sym[ii, :] / nat
BC_cdw += R_cdw[ii, :] / nat
R_cdw = (BC_sym - BC_cdw) + R_cdw
if at_cdw != at_sym:
if comm.rank == 0:
file.write('Atom order does not match. Starting permutation...\n')
R_cdw, at_cdw = permutation_finder(nat, R_cdw, R_sym, at_cdw, at_sym,
eps=0.5 * a)
if at_cdw != at_sym:
if comm.rank == 0:
file.write('Atom order still does not match. Stopping program...\n')
sys.exit()
"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""
# Calculate some important distances:
"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""
# Total displacement vector
U_tot = np.sqrt(((R_cdw - R_sym) ** 2).sum())
if comm.rank == 0:
file.write('Total displacement vector (angstrom): U = %3.4f\n' % U_tot)
distance = np.empty((nat))
for atom_index in range(nat):
distance[atom_index] = np.linalg.norm(R_cdw[atom_index] - R_sym[atom_index])
if comm.rank == 0:
file.write('Maximal displacement of %s atom is %1.2f %s\n'
% (at_cdw[np.argmax(distance)], np.max(distance) / a * 100, '%'))
file.close()
# Plot structures
if comm.rank != 0:
raise SystemExit
for atom_index in range(nat):
if at_sym[atom_index] == transition_metal:
plt.plot(R_sym[atom_index, 0], R_sym[atom_index, 1], 'o',
color='cyan', markersize=15)
elif at_sym[atom_index] == chalcogen:
plt.plot(R_sym[atom_index, 0], R_sym[atom_index, 1], 'o',
color='orangered', markersize=15)
for atom_index in range(nat):
if at_cdw[atom_index] == transition_metal:
plt.plot(R_cdw[atom_index, 0], R_cdw[atom_index, 1], 'o',
color='darkblue', markersize=15)
elif at_cdw[atom_index] == chalcogen:
plt.plot(R_cdw[atom_index, 0], R_cdw[atom_index, 1], 'o',
color='gold', markersize=15)
Start_Pos = (0, 0)
plt.plot([0, A1[0]], [0, A1[1]], color='black')
plt.plot([0, A2[0]], [0, A2[1]], color='black')
plt.plot([0, A1[0]], [0, A1[1]], color='black')
plt.plot([0, A2[0]], [0, A2[1]], color='black')
plt.plot([Start_Pos[0] + A2[0], Start_Pos[0] + A2[0] + A1[0]],
[Start_Pos[1] + A2[1], Start_Pos[1] + A2[1] + A1[1]], color='black')
plt.plot([Start_Pos[0] + A1[0], Start_Pos[0] + A2[0] + A1[0]],
[Start_Pos[1] + A1[1], Start_Pos[1] + A2[1] + A1[1]], color='black')
plt.axis('off')
plt.axis('equal')
plt.savefig('modes.png')
plt.show()