Long-range terms

This example verifies that PHonon, EPW, and elphmod yield identical long-range terms for phonons and coupling.

The values of the quadrupole tensors originate from Poncé, Royo, Gibertini, Marzari, and Stengel, Accurate prediction of Hall mobilities in two-dimensional materials through gauge-covariant quadrupolar contributions Phys. Rev. Lett. 130, 166301 (2023).

#!/usr/bin/env python3

# Copyright (C) 2017-2025 elphmod Developers
# This program is free software under the terms of the GNU GPLv3 or later.

import elphmod
import matplotlib.pyplot as plt
import numpy as np
import sys

comm = elphmod.MPI.comm

path = 'KGM'
q, x, corners = elphmod.bravais.path(path, ibrav=4, N=50, moveG=0.1)

if len(sys.argv) > 1 and sys.argv[1] == '--prepare-q':
    if comm.rank == 0:
        q /= 2 * np.pi
        weight = 1 / len(q)

        with open('q.dat', 'w') as filqf:
            filqf.write('%d crystal\n' % len(q))

            for q1, q2, q3 in q:
                filqf.write('%12.10f %12.10f %12.10f %12.10f\n'
                    % (q1, q2, q3, weight))

        for lr in '3d', 'gaussian':
            elphmod.bravais.write_matdyn('matdyn_%s.in' % lr, dict(
                flfrc='%s.ifc' % lr,
                flfrq='%s.freq' % lr,
                nq=len(q),
                q=q,
                q_in_cryst_coord=True,
                asr='simple',
                loto_2d=lr != '3d',
                fldos=' ',
                fleig=' ',
                flvec=' ',
            ))

    raise SystemExit

number = iter(range(1, 99))

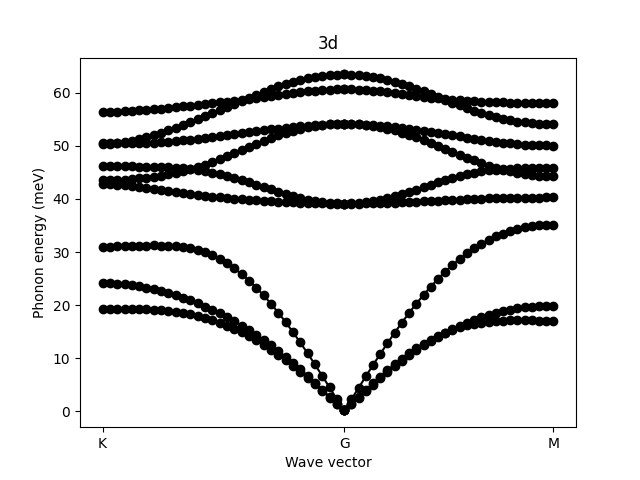
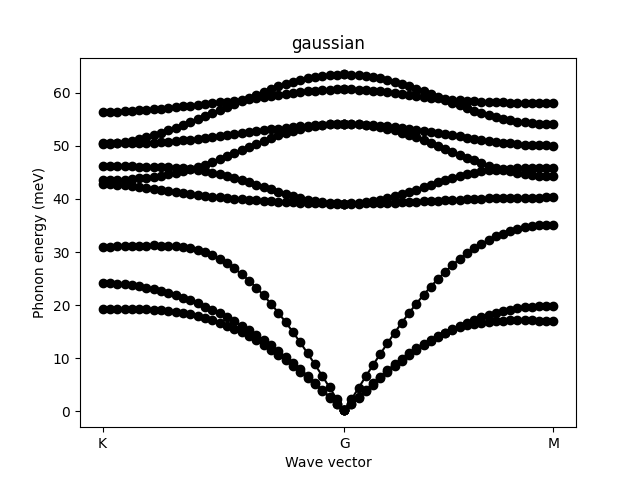
for lr in '3d', 'gaussian':
    ph = elphmod.ph.Model('%s.ifc' % lr, apply_asr_simple=True, apply_zasr=True,
        lr2d=lr != '3d', lr=True)

    if '3d' in lr:
        ph.prepare_long_range(G_2d=True)

    w = elphmod.ph.sgnsqrt(elphmod.dispersion.dispersion(ph.D, q))

    q0, x0, w0 = elphmod.el.read_bands('%s.freq' % lr)

    if comm.rank == 0:
        plt.plot(x, w0.T * 1e3 * elphmod.misc.cmm1, 'ok')
        plt.plot(x, w * 1e3 * elphmod.misc.Ry, '-k')

        plt.title(lr)
        plt.ylabel('Phonon energy (meV)')
        plt.xlabel('Wave vector')
        plt.xticks(x[corners], path)
        plt.savefig('lr_%d.png' % next(number))
        plt.show()

el = elphmod.el.Model('MoS2')

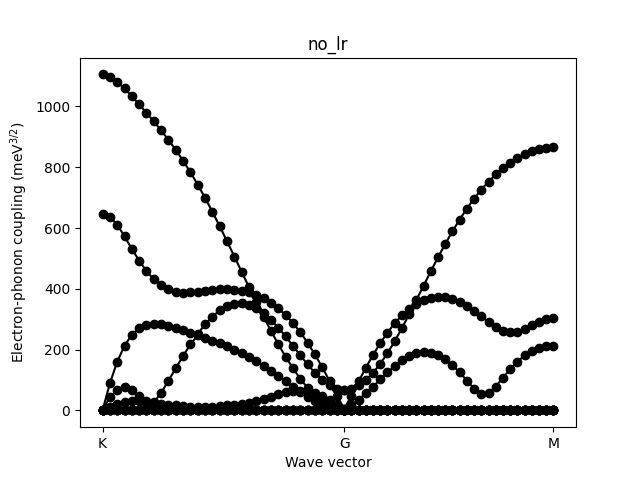
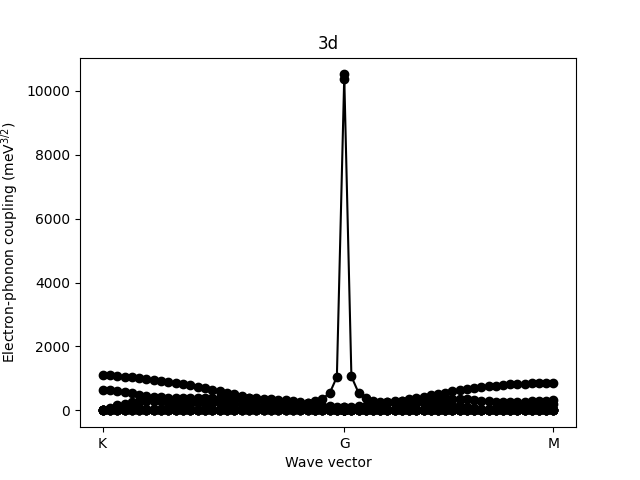
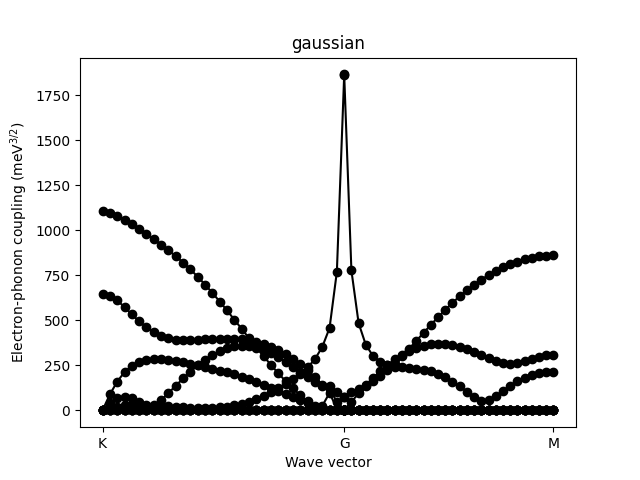
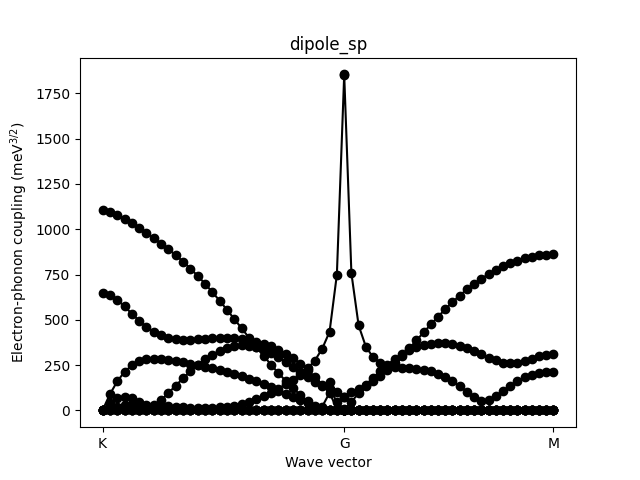
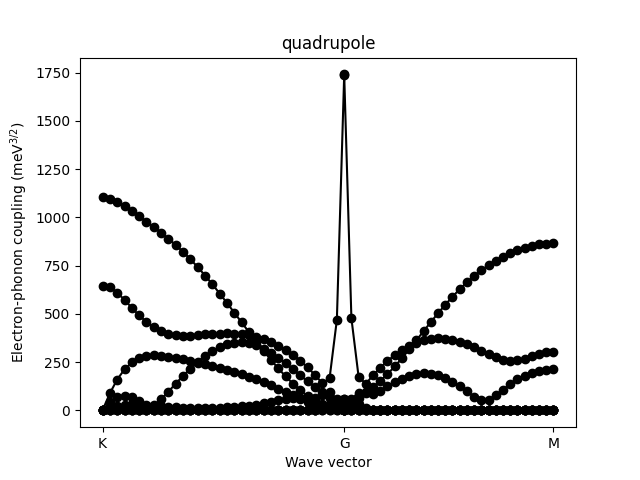
for lr in 'no_lr', '3d', 'gaussian', 'dipole_sp', 'quadrupole':
    ph = elphmod.ph.Model('dyn', apply_asr_simple=True, apply_zasr=True,
        lr=lr != 'no_lr',
        lr2d=lr != '3d',
        L=elphmod.elph.read_L('epw_%s.out' % lr),
        quadrupole_fmt='_quadrupole.fmt' if lr == 'quadrupole' else None)

    if '3d' in lr:
        ph.prepare_long_range(G_2d=True)

    elph = elphmod.elph.Model('%s.epmatwp' % lr, 'wigner.fmt', el, ph)

    g = np.absolute([elph.g(q1, q2, q3, elbnd=True, phbnd=True)
        for q1, q2, q3 in q])

    g = np.sort(g, axis=1)

    w0, g0 = elphmod.elph.read_prtgkk('epw_%s.out' % lr,
        nq=len(q), nmodes=ph.size, nk=1, nbnd=el.size)

    if comm.rank == 0:
        plt.plot(x, elphmod.ph.sgnsqrt(2 * w0) * g0[:, :, 0, 0, 0], 'ok')
        plt.plot(x, g[:, :, 0, 0] * (1e3 * elphmod.misc.Ry) ** 1.5, '-k')

        plt.title(lr)
        plt.ylabel('Electron-phonon coupling (meV$^{3 / 2}$)')
        plt.xlabel('Wave vector')
        plt.xticks(x[corners], path)
        plt.savefig('lr_%d.png' % next(number))
        plt.show()