Double delta (nesting function)

#!/usr/bin/env python3

# Copyright (C) 2017-2025 elphmod Developers
# This program is free software under the terms of the GNU GPLv3 or later.

import elphmod
import matplotlib.pyplot as plt
import numpy as np

comm = elphmod.MPI.comm

mu = -0.1665

nk = 120
dk = 12
nq = nk

kT = 0.01

el = elphmod.el.Model('data/NbSe2')

ekk = elphmod.dispersion.dispersion_full(el.H, nk)[:, :, :1] - mu
Ekk = ekk[::dk, ::dk, 0]

q = np.array(sorted(elphmod.bravais.irreducibles(nq)))

wedge = np.empty((len(q), 2))

wedge[:, 0] = elphmod.diagrams.double_fermi_surface_average(q * 2 * np.pi / nq,
    ekk, kT=kT)[1] / nk ** 2

progress = elphmod.misc.StatusBar(len(q),
    title='calculate double-delta integrals')

for iq, (q1, q2) in enumerate(q):
    ekq = np.roll(np.roll(ekk, shift=-q1, axis=0), shift=-q2, axis=1)
    Ekq = ekq[::dk, ::dk, 0]

    intersections = elphmod.dos.double_delta(Ekk, Ekq)(0.0)

    wedge[iq, 1] = sum(intersections.values())

    progress.update()

mesh = np.empty((nq, nq, 2))

for iq, (q1, q2) in enumerate(q):
    for q1, q2 in elphmod.bravais.images(q1, q2, nq):
        mesh[q1, q2] = wedge[iq]

if comm.rank == 0:
    figure, axes = plt.subplots(1, 2)

for n in range(2):
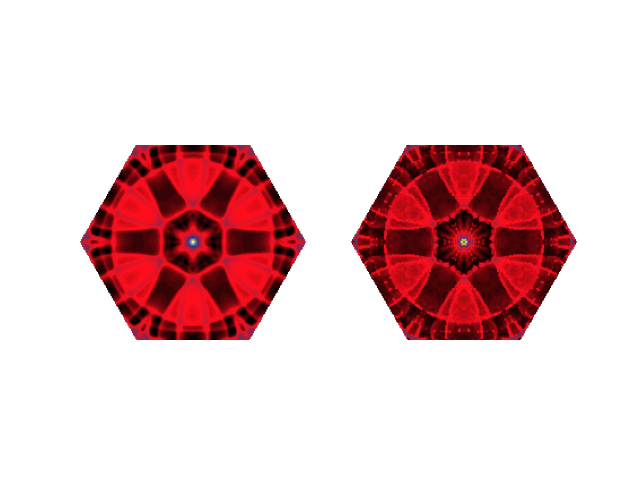
    BZ = elphmod.plot.toBZ(mesh[..., n], outside=np.nan, points=300)

    if comm.rank == 0:
        axes[n].imshow(BZ, cmap='gist_stern')
        axes[n].axis('image')
        axes[n].axis('off')

if comm.rank == 0:
    plt.savefig('double_delta.png')
    plt.show()