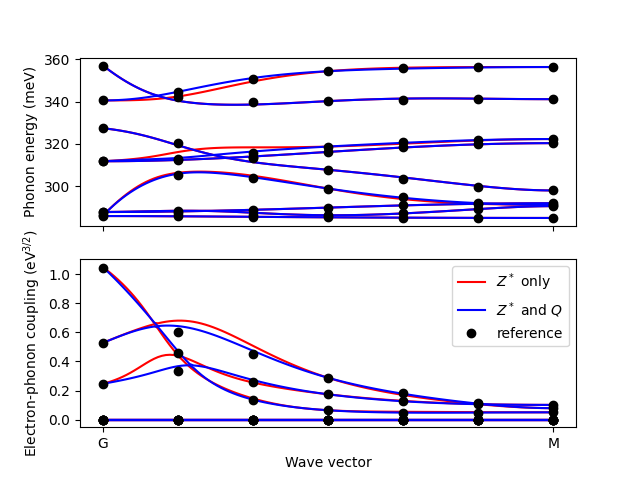
Quadrupole fitting
This is a minimal working example of the optimization of quadrupole tensors as done by J. Berges, N. Girotto, T. Wehling, N. Marzari, and S. Poncé, Phonon self-energy corrections: To screen, or not to screen, Phys. Rev. X 13, 041009 (2023). The original version can be found here.
More precisely, we first calculate (bare) dynamical matrices and electron-phonon matrix elements both on a coarse q mesh and for selected q points along a path. Then we Fourier interpolate the former, minimizing deviations from the latter. Here, the free parameters are the independent elements of the quadrupole tensors Q and the range-separation parameter L entering the formulas for the long-range components that are subtracted and added before and after interpolation. First, we optimize L for Q = 0, minimizing the short-range part of the force constants. Second, we optimize Q for constant L. A simultaneous optimization would also be possible, but it is only important that L is in the correct range.
For the bare phonons, you need a modified version of Quantum ESPRESSO. You can use the provided patches to apply the required changes.
Note that the results obtained in this example are not converged. The parameters have been chosen such that the calculations can be done on a personal computer.
#!/usr/bin/env python3
import elphmod
import matplotlib.pyplot as plt
import numpy as np
import scipy.optimize
comm = elphmod.MPI.comm
info = elphmod.MPI.info
info('Load tight-binding, mass-spring, and coupling models')
el = elphmod.el.Model('TaS2')
ph = elphmod.ph.Model('dyn', lr=False)
elph = elphmod.elph.Model('work/TaS2.epmatwp', 'wigner.fmt', el, ph)
elph.sample_orig()
info('Set up q-point path')
path = 'GM'
q, x, corners = elphmod.bravais.path(path, ibrav=4, N=198, moveG=1e-2)
q0, x0, w0 = elphmod.el.read_bands('dynref.freq')
q0 = 2 * np.pi * np.dot(q0, ph.a.T) / np.linalg.norm(ph.a[0])
x0 += x[-1] - x0[-1]
info('Load reference data')
sqrtM = np.sqrt(np.repeat(ph.M, 3))
D0 = np.empty((len(q0), ph.size, ph.size), dtype=complex)
for iq in range(len(q0)):
D0[iq] = elphmod.ph.read_flfrc('dynref%d' % (iq + 1))[0][1][0]
D0 /= sqrtM[np.newaxis, np.newaxis, :]
D0 /= sqrtM[np.newaxis, :, np.newaxis]
g0 = np.empty((len(q0), ph.size), dtype=complex)
iq = 0
with open('phref.out') as lines:
for line in lines:
if 'Printing the electron-phonon matrix elements' in line:
next(lines)
next(lines)
for line in lines:
cols = line.split()
if not cols:
break
i, m, n, k1, k2, k3 = tuple(map(int, cols[:6]))
if m == n == 13 and k1 == k2 == k3 == 0:
g0[iq, i - 1] = float(cols[6]) + 1j * float(cols[7])
iq += 1
g0 /= sqrtM[np.newaxis, :]
info('Optimize long-range separation parameter')
ph.lr = True
def objective(L):
ph.L, = L
ph.update_short_range()
return ph.sum_force_constants()
scipy.optimize.minimize(objective, [1.0], tol=0.1)
elph.update_short_range()
info('Interpolate dynamical matrix and coupling for Q = 0')
def sample(q):
D = elphmod.dispersion.sample(ph.D, q)
g = elphmod.dispersion.sample(elph.g, q, elbnd=True,
comm=elphmod.MPI.I)[:, :, 0, 0]
return D, g
Dd, gd = sample(q)
info('Optimze quadrupole tensors')
def error():
D, g = sample(q0)
dD = (abs(D - D0) ** 2).sum()
dg = (abs(abs(g) - abs(g0)) ** 2).sum()
return dD, dg
dD0, dg0 = error()
def objective(Q):
ph.Q = np.zeros((ph.nat, 3, 3, 3))
ph.Q[1, 1, 1, 1] = Q[0] # Ta y y y
ph.Q[2, 1, 1, 1] = Q[1] # S y y y
ph.Q[2, 2, 1, 1] = Q[2] # S z y y
ph.Q[:, 0, 0, 1] = ph.Q[:, 0, 1, 0] = ph.Q[:, 1, 0, 0] = -ph.Q[:, 1, 1, 1]
ph.Q[:, 2, 0, 0] = ph.Q[:, 2, 1, 1]
ph.Q[0, :2] = ph.Q[2, :2]
ph.Q[0, 2] = -ph.Q[2, 2]
ph.Q[Q == 0.0] = 0.0 # avoid negative zeros
ph.update_short_range()
elph.update_short_range()
dD, dg = error()
dD /= dD0
dg /= dg0
info('error(D) = %.10g%%' % (100 * dD))
info('error(g) = %.10g%%' % (100 * dg))
return np.sqrt(dD ** 2 + dg ** 2)
scipy.optimize.minimize(objective, np.ones(3), tol=1e-3)
info('Interpolate dynamical matrix and coupling for optimal Q')
Dq, gq = sample(q)
info('Plot results')
if comm.rank != 0:
raise SystemExit
elphmod.ph.write_quadrupole_fmt('quadrupole.fmt', ph.Q)
fig, (ax1, ax2) = plt.subplots(2, 1, sharex=True)
wd2, ud = np.linalg.eigh(Dd)
wq2, uq = np.linalg.eigh(Dq)
w02, u0 = np.linalg.eigh(D0)
ax1.plot(x, elphmod.ph.sgnsqrt(wd2) * 1e3 * elphmod.misc.Ry, 'r')
ax1.plot(x, elphmod.ph.sgnsqrt(wq2) * 1e3 * elphmod.misc.Ry, 'b')
ax1.plot(x0, elphmod.ph.sgnsqrt(w02) * 1e3 * elphmod.misc.Ry, 'ko')
gd = np.einsum('qx,qxv->qv', gd, ud)
gq = np.einsum('qx,qxv->qv', gq, uq)
g0 = np.einsum('qx,qxv->qv', g0, u0)
gd = np.sort(abs(gd), axis=1)
gq = np.sort(abs(gq), axis=1)
g0 = np.sort(abs(g0), axis=1)
for nu in range(ph.size):
ax2.plot(x, gd[:, nu] * elphmod.misc.Ry ** 1.5, 'r',
label=None if nu else '$Z^*$ only')
for nu in range(ph.size):
ax2.plot(x, gq[:, nu] * elphmod.misc.Ry ** 1.5, 'b',
label=None if nu else '$Z^*$ and $Q$')
for nu in range(ph.size):
ax2.plot(x0, g0[:, nu] * elphmod.misc.Ry ** 1.5, 'ko',
label=None if nu else 'reference')
ax1.set_ylabel('Phonon energy (meV)')
ax2.set_ylabel('Electron-phonon coupling (eV$^{3/2}$)')
ax2.set_xlabel('Wave vector')
ax2.set_xticks(x[corners])
ax2.set_xticklabels(path)
ax2.legend()
plt.savefig('quadrupole.png')
plt.show()